Kilka uwag o algorytmach

Algorytmem nazywa się przepis postępowania, prowadzący w sposób automatyczny do rozwiązania określonego problemu. Przepis ten powinien być na tyle precyzyjny, aby posługiwanie się nim polegało wyłącznie na wykonywaniu jego instrukcji. Zakłada się przy tym, że pewne instrukcje pierwotne tego przepisu są wykonalne tzn., ze są uprzednio zdefiniowane.

Każdy algorytm można opisać w sposób słówny używając poleceń typu: wykonaj...; jeśli jest prawdą..., to wykonaj...; zakończ; zacznij od początku; itd. Najła- twiejsze i najbardziej zrozumiałe jest przedstawienie al- gorytmu w postaci graficznej (schematów blokowych), zgodnej z ogólnie przyjętą konwencją. I tak opis instruk- cji (wykonaj...) umieszcza się zazwyczaj w prostokącie rys. 1a, testy (jeśli jest prawdą..., to wykonaj...) w rom- bach lub sześciokątach rys. 1b, a oznaczenie startu i sto- pu algorytmu w okręgach rys. 1c. Niekiedy wyróżnia się także polecenia wprowadzania informacji z zewnątrz (np. z klawiatury lub dysku) i wyprowadzania jej (np. na monitor lub drukarkę). Umieszcza się je wówczas w elementach przedstawionych na rys. 1d.

Poszczególne elementy opisu graficznego łączy się ze sobą strzałkami, które określają kolejność opera- cji wykonywanych w algorytmie. Strzałki wychodzące z pól opisu testu są etykietowane słowami "tak" lub "nie" i wskazują na następne czynności w zależności od wyniku testu.

Instrukcje lub testy mogą być opisywane słownie lub za pomocą wyrażeń i symboli. Im bardziej opis al- gorytmu jest sformalizowany, tzn. zapisany w konwen- cji pewnego języka programowania, tym łatwiejsze jest przejście od algorytmu do programu. Przekształcanie algorytmu w program (w określonym języku programo- wania) to często bardzo pracochłonne zajęcie, lecz jest wyłącznie czynnością wtórną. Naprawdę twórcze jest napisanie prawidłowego algorytmu. Nieco upraszcza- jąc, możemy przyjąć, że prawidłowy algorytm to taki, który gwarantuje osiągnięcie postawionego celu zawsze w skończonej liczbie kroków. Każdy problem można rozwiązać na kilka różnych sposobów. Istnieje więc wiele algoryt mów. Jak spośród nich wybrać najlepszy, optymalny? Jeśli założymy, że najlepszy to ten, który doprowadza do celu po wykonaniu najmniejszej ilości operacji, to wybór staje się jednoznaczny.

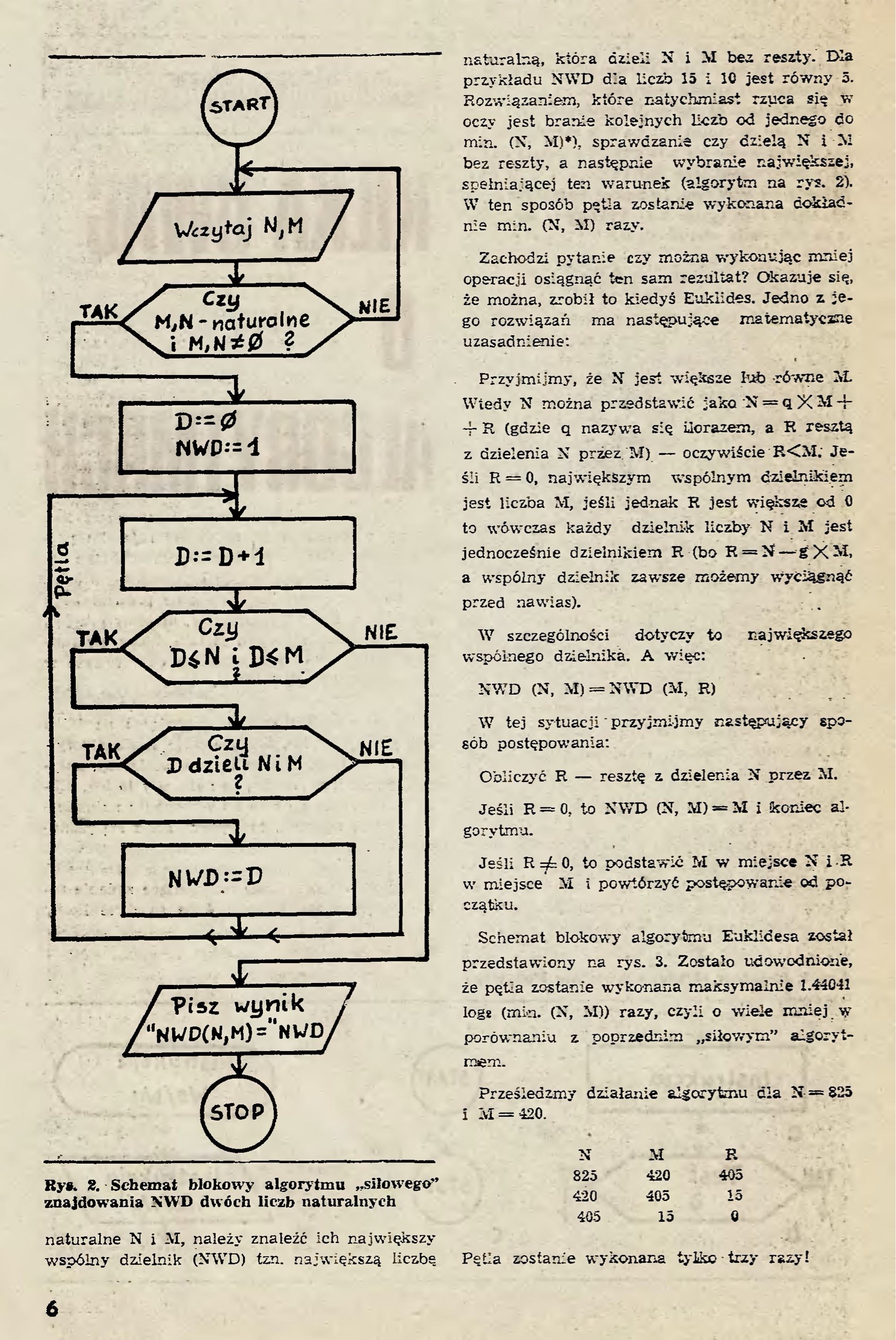
Spróbujmy rozwiązać następujące zadanie zaczerp- nięte x teorii liczb: dane są dwie liczby naturalne N i M, należy znaleźć ich największy wspólny dzielnik (NWD) tzn. największą liczbę naturalną, która dzieli N i M bez reszty. Dla przykładu NWD dla liczb 15 i 10 jest równy 5. Rozwiązaniem, które natychmiast rzuca się w oczy jest branie kolejnych liczb od jednego do min. (N, M)*), sprawdzanie czy dzielą N i M bez resz- ty, a następnie wybranie największej, spełniającej ten warunek (algorytm na rys. 2).

W ten sposób pętla zostanie wykonana dokładnie min. (N, M) razy.

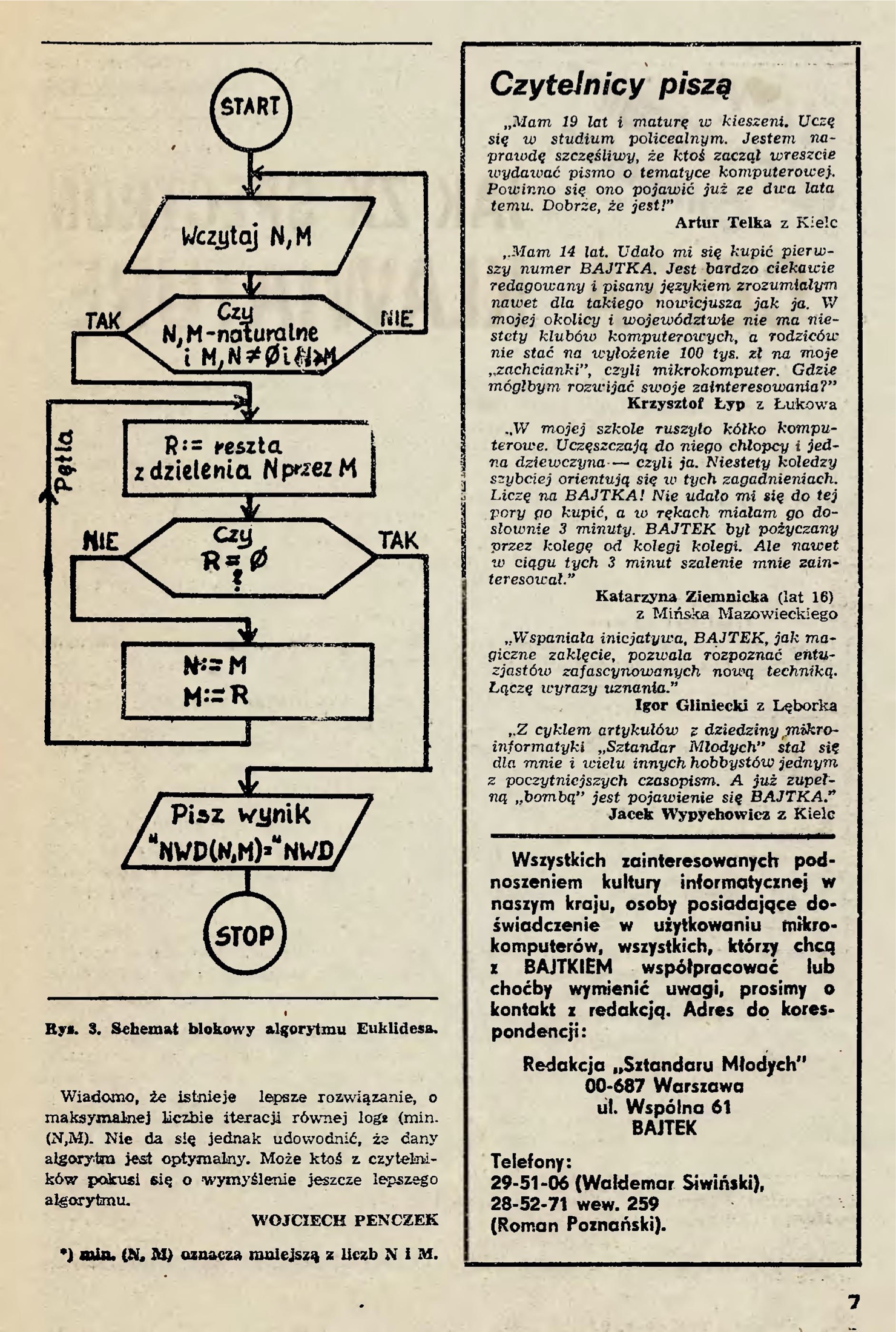
Zachodzi pytanie czy można wykonując mniej ope- racji osiągnąć ten sam rezultat? Okazuje się, że można, zrobił to kiedyś Euklides. Jedno z jego rozwiązań ma następujące matematyczne uzasadnienie:

Przyjmijmy, że N jest większe lub równe M. Wte- dy N można przedstawić jako N = q M + R (gdzie q nazywa się ilorazem, a R resztą z dzielenia N przez M) — oczywiście R<M. Jeśli R = 0, największym wspólnym dzielnikiem jest liczba M, jeśli jednak R jest większe od 0 to wówczas każdy dzielnik liczby N i M jest jed- nocześnie dzielnikiem R (bo R = N—q M), a wspól- ny dzielnik zawsze możemy wyciągnąć przed nawias). największego

W szczególności dotyczy to wspólnego dzielnika.

A więc:

NWD (N, M) = NWD (M, R)

W tej sytuacji przyjmijmy następujący sposób postępowania:

Obliczyć R — resztę z dzielenia N przez M. Jeśli R = 0, to NWD (N, M) = M i koniec algorytmu. Jeśli R!=0, to podstawić M w miejsce N i R w miej- sce M i powtórzyć postępowanie od początku.

Schemat blokowy algorytmu Euklidesa został przedstawiony na rys. 3. Zostało udowodnione, że pę- tla zostanie wykonana maksymalnie 1.44041 logs (min. (N, M)) razy, czyli o wiele mniej w porównaniu z po- przednim „siłowym" algorytmem.

Prześledźmy działanie algorytmu

dla N = 825 i M = 420

NMR 825 420 405 420 405 15 405 15 0

Pętla zostanie wykonana tylko trzy razy!

Wiadomo, że istnieje lepsze rozwiązanie, o maksy- malnej liczbie iteracji równej log2 (min. (N,M). Nie da się jednak udowodnić, że dany algorytm jest optymalny. Może ktoś z czytelników pokusi się o wymyślenie jesz- cze lepszego algorytmu.

WOJCIECH PENCZEK

*) min. (N, M) oznacza mniejszą z liczb N i M.